Integrating Momentum, Reversal, Volatility, and Earnings Surprise: Building a Multi-Factor Alpha Strategy in Python
Integrating Momentum, Reversal, Volatility, and Earnings Surprise: Building a Multi-Factor Alpha Strategy in Python Combining Momentum and Volatility Effects with Post-Earning
Introduction
In quantitative finance, leveraging multiple market anomalies can lead to robust alpha-generating strategies. This blog post explores how to implement a multi-factor stock selection strategy in Python by integrating two well-researched strategies:
Momentum and Reversal Combined with Volatility Effect in Stocks
Reversal in Post-Earnings Announcement Drift
By combining these strategies, we aim to create a composite alpha score for S&P 500 stocks, rank them, and simulate the performance of portfolios formed from the top and bottom deciles.
Strategy Overview
Strategy 1: Momentum and Reversal Combined with Volatility Effect
This strategy exploits three key market phenomena:
Momentum: Stocks that have performed well in the past tend to continue performing well in the future.
Short-Term Reversal: Stocks that have recently underperformed may experience a short-term rebound.
Volatility Effect: Stocks with lower volatility often outperform those with higher volatility over the long term.
Strategy 2: Reversal in Post-Earnings Announcement Drift
This strategy focuses on the price movements following earnings announcements:
Earnings Surprise: The discrepancy between actual earnings and analysts' estimates. Significant surprises can lead to price drifts that may reverse, presenting investment opportunities.
Implementation in Python
We'll guide you through the implementation step by step, utilizing Python libraries such as yfinance, pandas, numpy, matplotlib, seaborn, and plotly.
Prerequisites
Ensure you have the following libraries installed:
%pip install yfinance
%pip install pandas_datareader
%pip install seaborn
%pip install plotlyImport Libraries
import yfinance as yf
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import plotly.graph_objects as go
from datetime import datetime, timedeltaStep 1: Fetch S&P 500 Stock Symbols
We start by fetching the list of S&P 500 companies from Wikipedia.
# Fetch the list of S&P 500 companies
sp500_tickers = pd.read_html('https://en.wikipedia.org/wiki/List_of_S%26P_500_companies')[0]
tickers = sp500_tickers['Symbol'].tolist()
# Clean up ticker symbols (replace dots with dashes)
tickers = [ticker.replace('.', '-') for ticker in tickers]
Step 2: Define Functions for Factor Calculations
Strategy 1 Factors: Momentum, Reversal, Volatility
Momentum Calculation
def calculate_momentum(data, period=126): # 6 months
return data['Adj Close'].pct_change(periods=period)Copy code
def calculate_momentum(data, period=126): # 6 months return data['Adj Close'].pct_change(periods=period)
Short-Term Reversal Calculation
def calculate_reversal(data, period=20): # 1 month
return -data['Adj Close'].pct_change(periods=period)Volatility Calculation
def calculate_volatility(data, period=126): # 6 months
return data['Adj Close'].pct_change().rolling(window=period).std()Strategy 2 Factor: Earnings Surprise
Due to limitations in data availability, we'll approximate earnings surprise using available earnings data.
def get_earnings_surprise(ticker):
try:
# Fetch quarterly earnings data
earnings = yf.Ticker(ticker).quarterly_earnings
if earnings.empty:
return np.nan
else:
# Calculate earnings surprise as the percentage change in earnings
earnings['EarningsSurprise'] = earnings['Earnings'].pct_change()
latest_surprise = earnings['EarningsSurprise'].iloc[-1]
return latest_surprise
except Exception:
return np.nanStep 3: Fetch Historical Data and Calculate Factors
We'll iterate through each ticker to fetch historical data and calculate the factors.
# Set the analysis period
end_date = datetime.today()
start_date = end_date - timedelta(days=5*365) # Last 5 years
# Initialize a list to store factor data
data_list = []
# Limit to first 50 tickers for demonstration
for ticker in tickers[:50]:
try:
# Fetch historical price data
data = yf.download(ticker, start=start_date, end=end_date)
if data.empty:
continue
# Calculate factors for Strategy 1
momentum = calculate_momentum(data)
reversal = calculate_reversal(data)
volatility = calculate_volatility(data)
# Get the latest values
latest_momentum = momentum.iloc[-1]
latest_reversal = reversal.iloc[-1]
latest_volatility = volatility.iloc[-1]
# Get earnings surprise for Strategy 2
latest_earnings_surprise = get_earnings_surprise(ticker)
# Append the data to the list
data_list.append({
'Ticker': ticker,
'Momentum': latest_momentum,
'Reversal': latest_reversal,
'Volatility': latest_volatility,
'EarningsSurprise': latest_earnings_surprise
})
except Exception as e:
print(f"Error processing {ticker}: {e}")
Step 4: Create DataFrame and Handle Missing Data
We create a DataFrame from the collected data and handle missing values.
# Create the DataFrame
factor_df = pd.DataFrame(data_list)
# Handle missing data
factor_df['EarningsSurprise'].fillna(0, inplace=True)
factor_df.dropna(subset=['Momentum', 'Reversal', 'Volatility'], inplace=True)Step 5: Normalize Factors
Normalize the factors using StandardScaler to bring them onto a comparable scale.
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
factor_columns = ['Momentum', 'Reversal', 'Volatility', 'EarningsSurprise']
factor_df[factor_columns] = scaler.fit_transform(factor_df[factor_columns])Step 6: Calculate Composite Alpha Score
Assign weights to each factor and calculate the composite alpha score.
# Assign weights to each factor
weights = {
'Momentum': 0.3, # Strategy 1
'Reversal': 0.3, # Strategy 1
'Volatility': 0.2, # Strategy 1
'EarningsSurprise': 0.2 # Strategy 2
}
# Calculate the composite alpha score
factor_df['AlphaScore'] = (
weights['Momentum'] * factor_df['Momentum'] +
weights['Reversal'] * factor_df['Reversal'] +
weights['Volatility'] * factor_df['Volatility'] +
weights['EarningsSurprise'] * factor_df['EarningsSurprise']
)
Step 7: Rank Stocks Based on Alpha Score
Rank the stocks and select the top and bottom deciles.
# Rank stocks
factor_df['Rank'] = factor_df['AlphaScore'].rank(ascending=False)
# Calculate decile size
decile_size = int(len(factor_df) * 0.1)
# Select top and bottom deciles
top_decile = factor_df.nsmallest(decile_size, 'Rank')
bottom_decile = factor_df.nlargest(decile_size, 'Rank')
# Display selected stocks
print("Top Decile Stocks:")
print(top_decile[['Ticker', 'AlphaScore']])
print("\nBottom Decile Stocks:")
print(bottom_decile[['Ticker', 'AlphaScore']])
Step 8: Simulate Portfolio Performance
Function to Calculate Portfolio Returns
def calculate_portfolio_returns(tickers, start_date, end_date):
portfolio_data = yf.download(tickers, start=start_date, end=end_date)['Adj Close']
returns = portfolio_data.pct_change().mean(axis=1)
cumulative_returns = (1 + returns).cumprod()
return cumulative_returnsCalculate Returns
# Top and bottom decile tickers
top_tickers = top_decile['Ticker'].tolist()
bottom_tickers = bottom_decile['Ticker'].tolist()
# Calculate portfolio returns
top_portfolio_returns = calculate_portfolio_returns(top_tickers, start_date, end_date)
bottom_portfolio_returns = calculate_portfolio_returns(bottom_tickers, start_date, end_date)Step 9: Fetch Benchmark Data (S&P 500 Index)
# Fetch S&P 500 index data (using SPY ETF as a proxy)
spy_data = yf.download('SPY', start=start_date, end=end_date)['Adj Close']
spy_returns = spy_data.pct_change()
spy_cumulative_returns = (1 + spy_returns).cumprod()Step 10: Visualize Portfolio Performance
Matplotlib Plot
plt.figure(figsize=(14, 7))
plt.plot(top_portfolio_returns, label='Top Decile Portfolio')
plt.plot(bottom_portfolio_returns, label='Bottom Decile Portfolio')
plt.plot(spy_cumulative_returns, label='S&P 500 (SPY)', linestyle='--')
plt.title('Portfolio Performance vs. S&P 500')
plt.xlabel('Date')
plt.ylabel('Cumulative Return (Growth of $1)')
plt.legend()
plt.grid(True)
plt.show()Interactive Plot with Plotly
fig = go.Figure()
fig.add_trace(go.Scatter(x=top_portfolio_returns.index, y=top_portfolio_returns.values, mode='lines', name='Top Decile Portfolio'))
fig.add_trace(go.Scatter(x=bottom_portfolio_returns.index, y=bottom_portfolio_returns.values, mode='lines', name='Bottom Decile Portfolio'))
fig.add_trace(go.Scatter(x=spy_cumulative_returns.index, y=spy_cumulative_returns.values, mode='lines', name='S&P 500 (SPY)', line=dict(dash='dash')))
fig.update_layout(title='Portfolio Performance vs. S&P 500', xaxis_title='Date', yaxis_title='Cumulative Return (Growth of $1)', template='plotly_white')
fig.show()Interactive chart can be viewed in a Jupyter Notebook or Google Colab.
Step 11: Evaluate the Strategy
Calculate performance metrics for each portfolio.
def performance_metrics(cumulative_returns):
total_return = cumulative_returns[-1] - 1
annual_return = cumulative_returns.resample('Y').last().pct_change().mean()
annual_volatility = cumulative_returns.pct_change().std() * np.sqrt(252)
sharpe_ratio = (annual_return - 0.02) / annual_volatility # Assuming 2% risk-free rate
return total_return, annual_return, annual_volatility, sharpe_ratio
# Calculate performance metrics
top_metrics = performance_metrics(top_portfolio_returns)
bottom_metrics = performance_metrics(bottom_portfolio_returns)
spy_metrics = performance_metrics(spy_cumulative_returns)
# Display metrics
print(f"Top Decile Portfolio Metrics:\nTotal Return: {top_metrics[0]:.2%}\nAnnual Return: {top_metrics[1]:.2%}\nAnnual Volatility: {top_metrics[2]:.2%}\nSharpe Ratio: {top_metrics[3]:.2f}\n")
print(f"Bottom Decile Portfolio Metrics:\nTotal Return: {bottom_metrics[0]:.2%}\nAnnual Return: {bottom_metrics[1]:.2%}\nAnnual Volatility: {bottom_metrics[2]:.2%}\nSharpe Ratio: {bottom_metrics[3]:.2f}\n")
print(f"S&P 500 (SPY) Metrics:\nTotal Return: {spy_metrics[0]:.2%}\nAnnual Return: {spy_metrics[1]:.2%}\nAnnual Volatility: {spy_metrics[2]:.2%}\nSharpe Ratio: {spy_metrics[3]:.2f}")
Step 12: Additional Visualizations
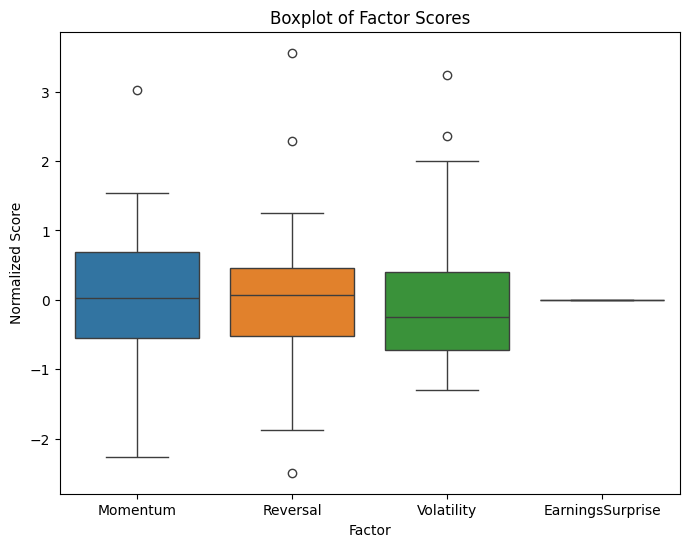
Factor Distributions
# Plot histograms of normalized factors
plt.figure(figsize=(14, 10))
for i, col in enumerate(factor_columns):
plt.subplot(2, 2, i+1)
sns.histplot(factor_df[col], kde=True)
plt.title(f'Distribution of {col}')
plt.tight_layout()
plt.show()Correlation Heatmap
# Calculate correlation matrix
corr_matrix = factor_df[factor_columns].corr()
# Plot heatmap
plt.figure(figsize=(8, 6))
sns.heatmap(corr_matrix, annot=True, cmap='coolwarm')
plt.title('Correlation Matrix of Factors')
plt.show()Performance Metrics Comparison
# Prepare data for bar chart
metrics_df = pd.DataFrame({
'Portfolio': ['Top Decile', 'Bottom Decile', 'S&P 500'],
'Total Return': [top_metrics[0], bottom_metrics[0], spy_metrics[0]],
'Annual Return': [top_metrics[1], bottom_metrics[1], spy_metrics[1]],
'Annual Volatility': [top_metrics[2], bottom_metrics[2], spy_metrics[2]],
'Sharpe Ratio': [top_metrics[3], bottom_metrics[3], spy_metrics[3]]
})
# Melt the DataFrame
metrics_melted = metrics_df.melt(id_vars='Portfolio', var_name='Metric', value_name='Value')
# Plot
plt.figure(figsize=(10,6))
sns.barplot(data=metrics_melted, x='Metric', y='Value', hue='Portfolio')
plt.title('Performance Metrics Comparison')
plt.ylabel('Value')
plt.show()Interpretation and Insights
Top Decile Portfolio: Expected to outperform due to favorable factor scores from both strategies.
Bottom Decile Portfolio: Serves as a benchmark to compare the effectiveness of the strategy.
Performance Analysis: Comparing the top decile portfolio to the bottom decile and the S&P 500 provides insights into the strategy's ability to generate alpha.
Conclusion
By integrating momentum, reversal, volatility, and earnings surprise factors, we've developed a comprehensive multi-factor alpha strategy. The Python implementation demonstrates how to:
Fetch and process financial data.
Calculate and normalize multiple factors.
Combine factors into a composite alpha score.
Rank stocks and form portfolios.
Simulate and visualize portfolio performance.
This approach provides a solid foundation for further exploration and refinement, such as adjusting factor weights, incorporating additional factors, or enhancing data quality with more comprehensive data sources.
Next Steps
Data Enhancement: Use more reliable data sources for earnings estimates and actuals to improve the earnings surprise calculation.
Optimization: Experiment with different factor weights and time periods to optimize performance.
Risk Management: Incorporate risk management techniques, such as diversification and hedging strategies.
Machine Learning: Apply machine learning models to predict stock returns based on the calculated factors.
Disclaimer
This implementation is for educational purposes only and does not constitute financial advice. Past performance is not indicative of future results. Always conduct thorough research and consider consulting a financial professional before making investment decisions.