Constructing an Enhanced Alpha Model using Momentum, Mean Reversion, and Sentiment Analysis Factors
Utilizing Momentum 1 Year, Mean Reversion 5 Day Sector Neutral Smoothed, and Overnight Sentiment Smoothed Factors to Improve Investment Performance
The objective of this project is to construct an improved Alpha, which is a measure of investment performance that evaluates returns beyond what could be expected from market movements. To achieve this, we will use a combination of three distinct factors: Momentum 1 Year Factor, Mean Reversion 5 Day Sector Neutral Smoothed Factor, and Overnight Sentiment Smoothed Factor.
The Momentum 1 Year Factor is a measure of a stock's recent performance over a one-year period. This factor identifies stocks that have demonstrated strong returns over the past year and involves buying them with the expectation that they will continue to perform well in the future.
The Mean Reversion 5 Day Sector Neutral Smoothed Factor focuses on identifying stocks that have experienced a recent dip in price and aims to capitalize on their tendency to revert back to their mean price. This factor is sector-neutral, which means that it is not biased towards any specific industry or sector, making it easier to use in diversified portfolios. Additionally, this factor is smoothed to reduce noise and make it easier to interpret.
The Overnight Sentiment Smoothed Factor analyzes news and social media sentiment to identify stocks that are likely to have positive price movements in the following day's trading session. This factor uses natural language processing techniques to analyze large amounts of data and smooths the results to reduce noise and increase accuracy.
Combining these three factors into an enhanced Alpha can help investors identify attractive investment opportunities that may have been overlooked by other market participants. It's worth noting that the selection and weighting of these factors will require careful consideration, and they may need to be refined and adjusted over time based on market conditions and performance.
Load Packages:
import numpy as np
import pandas as pd
from tqdm import tqdm
import matplotlib.pyplot as plt
%matplotlib inline
plt.style.use('ggplot')
plt.rcParams['figure.figsize'] = (14, 8)Data Pipeline
Data Bundle
We'll be using Zipline to handle our data. We've created a end of day data bundle for this project. Run the cell below to register this data bundle in zipline.
import os
from zipline.data import bundles
os.environ['ZIPLINE_ROOT'] = os.path.join(os.getcwd(), '..', '..', 'data', 'project_7_eod')
ingest_func = bundles.csvdir.csvdir_equities(['daily'], project_helper.EOD_BUNDLE_NAME)
bundles.register(project_helper.EOD_BUNDLE_NAME, ingest_func)
print('Data Registered')Build Pipeline Engine
We'll be using Zipline's pipeline package to access our data for this project. To use it, we must build a pipeline engine. Run the cell below to build the engine.
from zipline.pipeline import Pipeline
from zipline.pipeline.factors import AverageDollarVolume
from zipline.utils.calendars import get_calendar
universe = AverageDollarVolume(window_length=120).top(500)
trading_calendar = get_calendar('NYSE')
bundle_data = bundles.load(project_helper.EOD_BUNDLE_NAME)
engine = project_helper.build_pipeline_engine(bundle_data, trading_calendar)Alpha Factors
It's time to start working on the alpha factors. In this project, we'll use the following factors:
Momentum 1 Year Factor
Mean Reversion 5 Day Sector Neutral Smoothed Factor
Overnight Sentiment Smoothed Factor
from zipline.pipeline.factors import CustomFactor, DailyReturns, Returns, SimpleMovingAverage, AnnualizedVolatility
from zipline.pipeline.data import USEquityPricing
factor_start_date = universe_end_date - pd.DateOffset(years=3, days=2)
sector = project_helper.Sector()
def momentum_1yr(window_length, universe, sector):
return Returns(window_length=window_length, mask=universe) \
.demean(groupby=sector) \
.rank() \
.zscore()
def mean_reversion_5day_sector_neutral_smoothed(window_length, universe, sector):
unsmoothed_factor = -Returns(window_length=window_length, mask=universe) \
.demean(groupby=sector) \
.rank() \
.zscore()
return SimpleMovingAverage(inputs=[unsmoothed_factor], window_length=window_length) \
.rank() \
.zscore()
class CTO(Returns):
"""
Computes the overnight return, per hypothesis from
https://papers.ssrn.com/sol3/papers.cfm?abstract_id=2554010
"""
inputs = [USEquityPricing.open, USEquityPricing.close]
def compute(self, today, assets, out, opens, closes):
"""
The opens and closes matrix is 2 rows x N assets, with the most recent at the bottom.
As such, opens[-1] is the most recent open, and closes[0] is the earlier close
"""
out[:] = (opens[-1] - closes[0]) / closes[0]
class TrailingOvernightReturns(Returns):
"""
Sum of trailing 1m O/N returns
"""
window_safe = True
def compute(self, today, asset_ids, out, cto):
out[:] = np.nansum(cto, axis=0)
def overnight_sentiment_smoothed(cto_window_length, trail_overnight_returns_window_length, universe):
cto_out = CTO(mask=universe, window_length=cto_window_length)
unsmoothed_factor = TrailingOvernightReturns(inputs=[cto_out], window_length=trail_overnight_returns_window_length) \
.rank() \
.zscore()
return SimpleMovingAverage(inputs=[unsmoothed_factor], window_length=trail_overnight_returns_window_length) \
.rank() \
.zscore()Features and Labels
Let's create some features that we think will help the model make predictions.
"Universal" Quant Features
To capture the universe, we'll use the following as features:
Stock Volatility 20d, 120d
Stock Dollar Volume 20d, 120d
Sector
pipeline.add(AnnualizedVolatility(window_length=20, mask=universe).rank().zscore(), 'volatility_20d')
pipeline.add(AnnualizedVolatility(window_length=120, mask=universe).rank().zscore(), 'volatility_120d')
pipeline.add(AverageDollarVolume(window_length=20, mask=universe).rank().zscore(), 'adv_20d')
pipeline.add(AverageDollarVolume(window_length=120, mask=universe).rank().zscore(), 'adv_120d')
pipeline.add(sector, 'sector_code')Regime Features
We are going to try to capture market-wide regimes. To do that, we'll use the following features:
High and low volatility 20d, 120d
High and low dispersion 20d, 120d
class MarketDispersion(CustomFactor):
inputs = [DailyReturns()]
window_length = 1
window_safe = True
def compute(self, today, assets, out, returns):
# returns are days in rows, assets across columns
out[:] = np.sqrt(np.nanmean((returns - np.nanmean(returns))**2))
pipeline.add(SimpleMovingAverage(inputs=[MarketDispersion(mask=universe)], window_length=20), 'dispersion_20d')
pipeline.add(SimpleMovingAverage(inputs=[MarketDispersion(mask=universe)], window_length=120), 'dispersion_120d')Date Features
Let's make columns for the trees to split on that might capture trader/investor behavior due to calendar anomalies.
all_factors = engine.run_pipeline(pipeline, factor_start_date, universe_end_date)
all_factors['is_Janaury'] = all_factors.index.get_level_values(0).month == 1
all_factors['is_December'] = all_factors.index.get_level_values(0).month == 12
all_factors['weekday'] = all_factors.index.get_level_values(0).weekday
all_factors['quarter'] = all_factors.index.get_level_values(0).quarter
all_factors['qtr_yr'] = all_factors.quarter.astype('str') + '_' + all_factors.index.get_level_values(0).year.astype('str')
all_factors['month_end'] = all_factors.index.get_level_values(0).isin(pd.date_range(start=factor_start_date, end=universe_end_date, freq='BM'))
all_factors['month_start'] = all_factors.index.get_level_values(0).isin(pd.date_range(start=factor_start_date, end=universe_end_date, freq='BMS'))
all_factors['qtr_end'] = all_factors.index.get_level_values(0).isin(pd.date_range(start=factor_start_date, end=universe_end_date, freq='BQ'))
all_factors['qtr_start'] = all_factors.index.get_level_values(0).isin(pd.date_range(start=factor_start_date, end=universe_end_date, freq='BQS'))
all_factors.head()One Hot Encode Sectors
For the model to better understand the sector data, we'll one hot encode this data.
sector_lookup = pd.read_csv(
os.path.join(os.getcwd(), '..', '..', 'data', 'project_7_sector', 'labels.csv'),
index_col='Sector_i')['Sector'].to_dict()
sector_lookup
sector_columns = []
for sector_i, sector_name in sector_lookup.items():
secotr_column = 'sector_{}'.format(sector_name)
sector_columns.append(secotr_column)
all_factors[secotr_column] = (all_factors['sector_code'] == sector_i)
all_factors[sector_columns].head()Shift Target
We'll use shifted 5 day returns for training the model.
all_factors['target'] = all_factors.groupby(level=1)['return_5d'].shift(-5)
all_factors[['return_5d','target']].reset_index().sort_values(['level_1', 'level_0']).head(10)IID Check of Target
Let's see if the returns are independent and identically distributed.
from scipy.stats import spearmanr
def sp(group, col1_name, col2_name):
x = group[col1_name]
y = group[col2_name]
return spearmanr(x, y)[0]
all_factors['target_p'] = all_factors.groupby(level=1)['return_5d_p'].shift(-5)
all_factors['target_1'] = all_factors.groupby(level=1)['return_5d'].shift(-4)
all_factors['target_2'] = all_factors.groupby(level=1)['return_5d'].shift(-3)
all_factors['target_3'] = all_factors.groupby(level=1)['return_5d'].shift(-2)
all_factors['target_4'] = all_factors.groupby(level=1)['return_5d'].shift(-1)
g = all_factors.dropna().groupby(level=0)
for i in range(4):
label = 'target_'+str(i+1)
ic = g.apply(sp, 'target', label)
ic.plot(ylim=(-1, 1), label=label)
plt.legend(bbox_to_anchor=(1.04, 1), borderaxespad=0)
plt.title('Rolling Autocorrelation of Labels Shifted 1,2,3,4 Days')
plt.show()Train/Valid/Test Splits
Now let's split the data into a train, validation, and test dataset. Implement the function train_valid_test_split to split the input samples, all_x, and targets values, all_y into a train, validation, and test dataset. The proportion sizes are train_size, valid_size, test_size respectively.
When splitting, make sure the data is in order from train, validation, and test respectivly. Say train_size is 0.7, valid_size is 0.2, and test_size is 0.1. The first 70 percent of all_x and all_y would be the train set. The next 20 percent of all_x and all_y would be the validation set. The last 10 percent of all_x and all_y would be the test set. Make sure not split a day between multiple datasets. It should be contained within a single dataset.
def train_valid_test_split(all_x, all_y, train_size, valid_size, test_size):
"""
Generate the train, validation, and test dataset.
Parameters
----------
all_x : DataFrame
All the input samples
all_y : Pandas Series
All the target values
train_size : float
The proportion of the data used for the training dataset
valid_size : float
The proportion of the data used for the validation dataset
test_size : float
The proportion of the data used for the test dataset
Returns
-------
x_train : DataFrame
The train input samples
x_valid : DataFrame
The validation input samples
x_test : DataFrame
The test input samples
y_train : Pandas Series
The train target values
y_valid : Pandas Series
The validation target values
y_test : Pandas Series
The test target values
"""
assert train_size >= 0 and train_size <= 1.0
assert valid_size >= 0 and valid_size <= 1.0
assert test_size >= 0 and test_size <= 1.0
assert train_size + valid_size + test_size == 1.0
# TODO: Implement
NN = all_x.index.levels[0]
N = len(NN)
Tsx = int(N * train_size)
Vsx = int(N * (train_size + valid_size))
TRi = NN[:Tsx]
Vi = NN[Tsx:Vsx]
TEi = NN[Vsx:]
xTr, xV, xTe = all_x.loc[TRi[0]:TRi[-1]], all_x.loc[Vi[0]:Vi[-1]], all_x.loc[TEi[0]:TEi[-1]]
yTr, yV, yTe = all_y.loc[TRi[0]:TRi[-1]], all_y.loc[Vi[0]:Vi[-1]], all_y.loc[TEi[0]:TEi[-1]]
return xTr, xV, xTe, yTr, yV, yTeRandom Forests
Visualize a Simple Tree
Let's see how a single tree would look using our data.
from IPython.display import display
from sklearn.tree import DecisionTreeClassifier
# This is to get consistent results between each run.
clf_random_state = 0
simple_clf = DecisionTreeClassifier(
max_depth=3,
criterion='entropy',
random_state=clf_random_state)
simple_clf.fit(X_train, y_train)
display(project_helper.plot_tree_classifier(simple_clf, feature_names=features))
project_helper.rank_features_by_importance(simple_clf.feature_importances_, features)Model Results
Let's look at some additional metrics to see how well a model performs. We've created the function show_sample_results to show the following results of a model:
Sharpe Ratios
Factor Returns
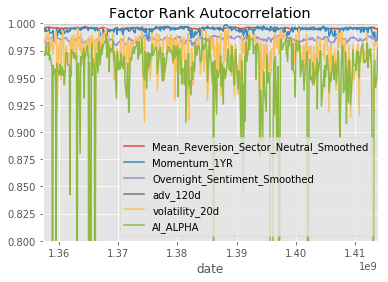
Factor Rank Autocorrelation
import alphalens as al
all_assets = all_factors.index.levels[1].values.tolist()
all_pricing = get_pricing(
data_portal,
trading_calendar,
all_assets,
factor_start_date,
universe_end_date)
def show_sample_results(data, samples, classifier, factors, pricing=all_pricing):
# Calculate the Alpha Score
prob_array=[-1,1]
alpha_score = classifier.predict_proba(samples).dot(np.array(prob_array))
# Add Alpha Score to rest of the factors
alpha_score_label = 'AI_ALPHA'
factors_with_alpha = data.loc[samples.index].copy()
factors_with_alpha[alpha_score_label] = alpha_score
# Setup data for AlphaLens
print('Cleaning Data...\n')
factor_data = project_helper.build_factor_data(factors_with_alpha[factors + [alpha_score_label]], pricing)
print('\n-----------------------\n')
# Calculate Factor Returns and Sharpe Ratio
factor_returns = project_helper.get_factor_returns(factor_data)
sharpe_ratio = project_helper.sharpe_ratio(factor_returns)
# Show Results
print(' Sharpe Ratios')
print(sharpe_ratio.round(2))
project_helper.plot_factor_returns(factor_returns)
project_helper.plot_factor_rank_autocorrelation(factor_data)Hopefully, you're impressed by this outcome. Even though there were notable variations in factor performances across the three sets, AI ALPHA managed to achieve a favorable result.